reading-notes

Trees

Collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the “children”), with the constraints that no reference is duplicated, and none points to the root.

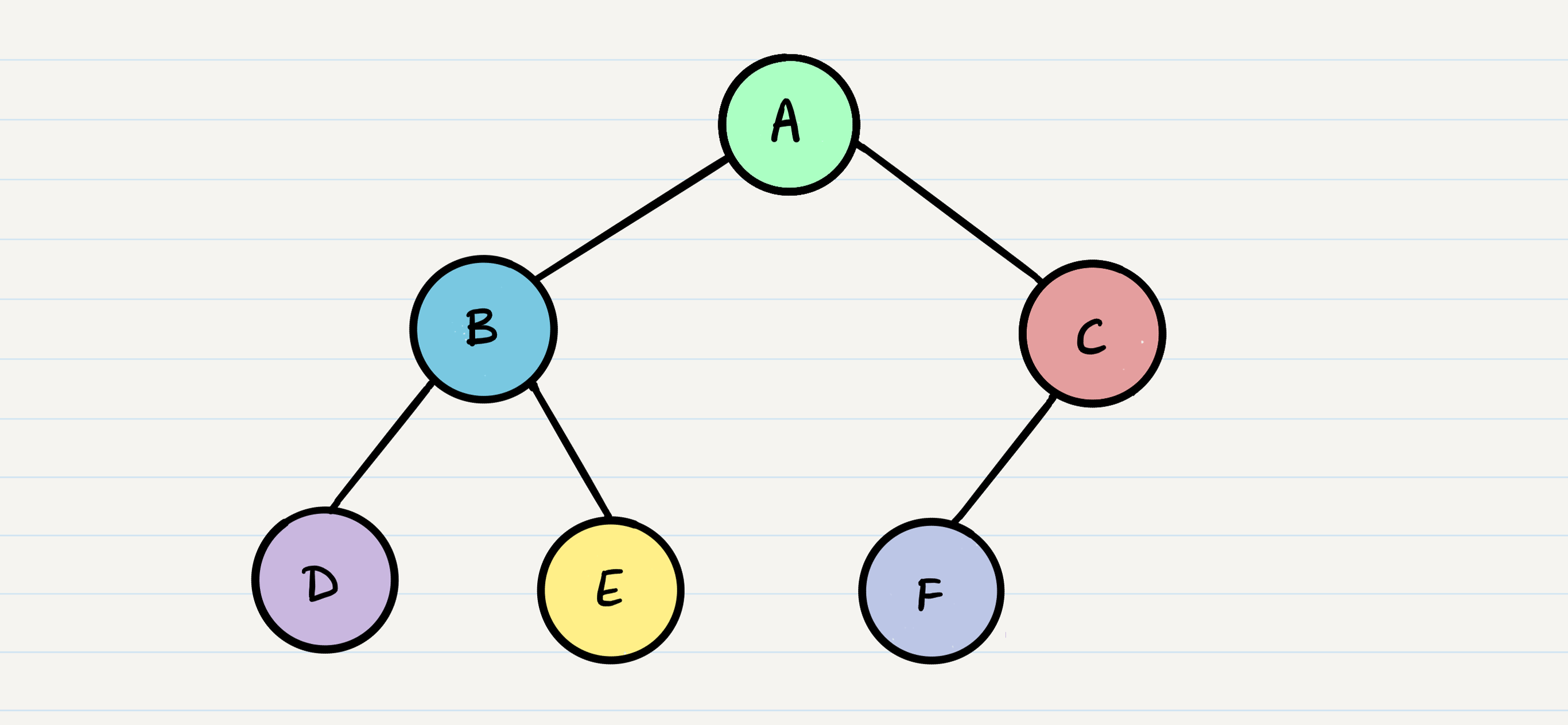
Simple Tree Example

Traversals

An important aspect of trees is how to traverse them. Traversing a tree allows us to search for a node, print out the contents of a tree, and much more! There are two categories of traversals when it comes to trees:

• Depth First
• Breadth First

Depth First

Depth first traversal is where we prioritize going through the depth (height) of the tree first. There are multiple ways to carry out depth first traversal, and each method changes the order in which we search/print the root. Here are three methods for depth first traversal:

• Pre-order: root » left » right
• In-order: left » root » right
• Post-order: left » right » root

Breadth First

Breadth first traversal iterates through the tree by going through each level of the tree node-by-node. So, given our starting tree one more time:

Binary Trees

Trees can have any number of children per node, but Binary Trees restrict the number of children to two (hence our left and right children).

Adding a node

Because there are no structural rules for where nodes are “supposed to go” in a binary tree, it really doesn’t matter where a new node gets placed.

One strategy for adding a new node to a binary tree is to fill all “child” spots from the top down. To do so, we would leverage the use of breadth first traversal. During the traversal, we find the first node that does not have 2 child nodes, and insert the new node as a child. We fill the child slots from left to right.

In the event you would like to have a node placed in a specific location, you need to reference both the new node to create, and the parent node upon which the child is attached to.

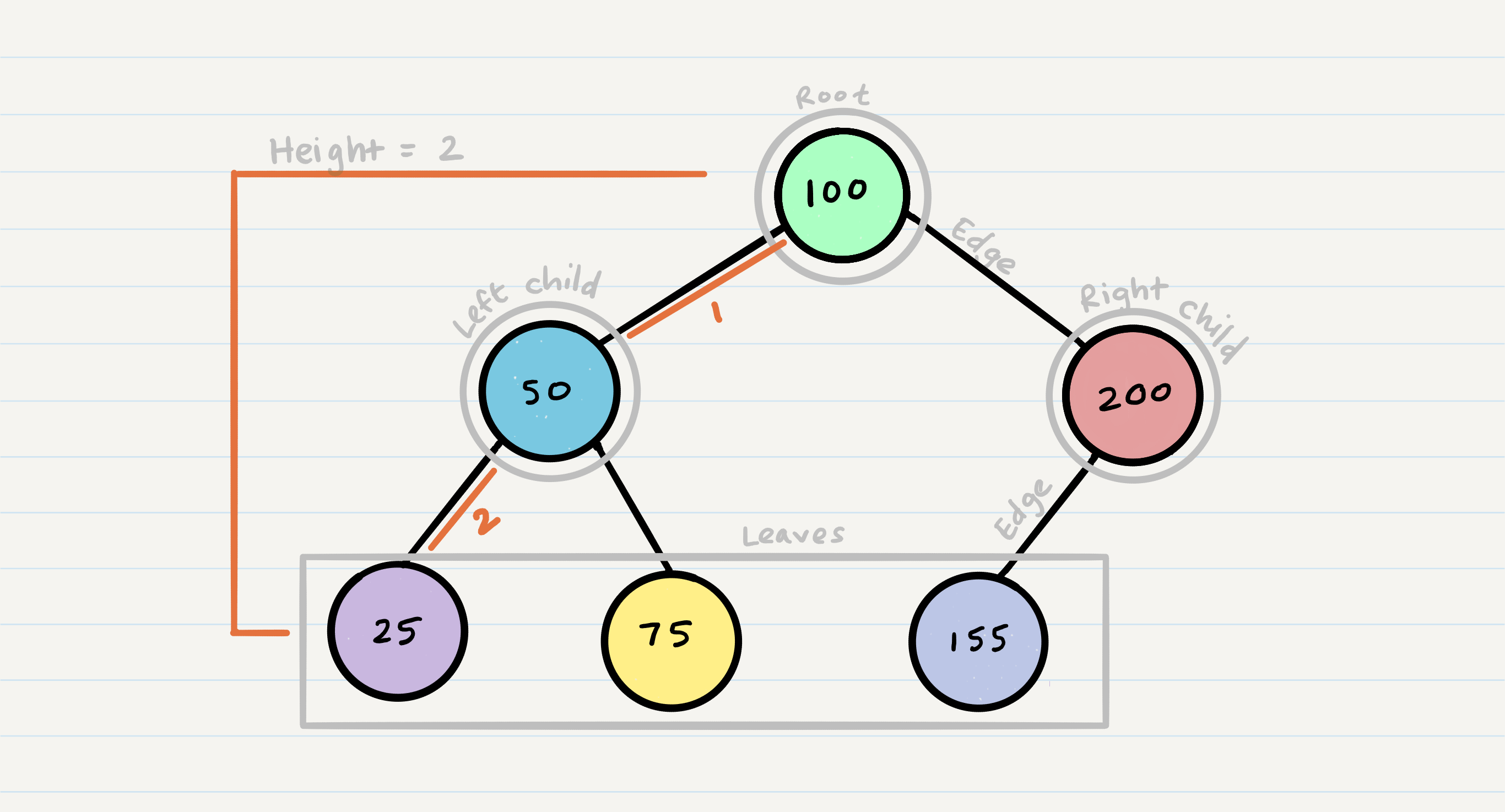
Binary Search Trees

A Binary Search Tree (BST) is a type of tree that does have some structure attached to it. In a BST, nodes are organized in a manner where all values that are smaller than the root are placed to the left, and all values that are larger than the root are placed to the right.